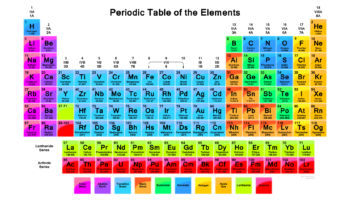
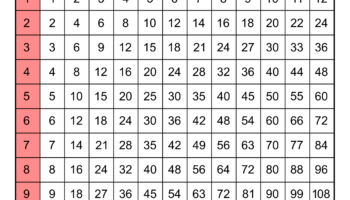
Assigning colors to numerals, integers, or elements within a numeric sequence constitutes a visual encoding technique used across varied disciplines. This method aids in distinguishing patterns, highlighting relationships, and simplifying complex data sets. For example, in mathematics, prime numbers could be represented by a specific color, while composite numbers receive another. Similarly, in data visualization, higher values might be shaded darker and lower values lighter, creating a color gradient that reveals trends quickly. The purpose of this assignment is not purely aesthetic; it is intended to enhance cognitive processing and facilitate quicker comprehension. This visual representation serves as a layer of abstraction, translating numerical data into a more readily digestible form, allowing for quicker identification of outliers, clusters, or correlations that might be missed when looking at raw numbers alone. The strategic use of color becomes a key element in translating abstract information into a more human-interpretable format.
The use of visual encoding in numerical datasets stems from a need to improve understanding and recognition. The benefits are far-reaching, impacting fields such as finance, scientific research, and education. In financial analysis, for instance, color-coded stock charts enable investors to quickly assess market trends and identify profitable opportunities. In scientific contexts, visualizing data from experiments can reveal previously unnoticed connections and accelerate the process of discovery. Educators also employ this technique to make abstract mathematical concepts more accessible to students. Color assignments can help students quickly grasp the relationships between numbers, such as prime factorization or the distribution of numbers in a sequence. The historical roots of this visualization can be traced back to early attempts at statistical graphics. The ability to represent quantities visually using shades or hues has always been a powerful way to communicate complex data to a wider audience.
The subsequent discussion will explore the application of visual encoding in various contexts. This includes its utilization in mathematical problem-solving, specifically addressing scenarios where strategic assignments help simplify complex equations or reveal underlying structures. Additionally, the exploration extends to its role in data analysis, where the assignment is critical for identifying patterns, clusters, and outliers in large datasets. We will also consider the pedagogical aspects, specifically how this method can enhance learning and understanding of mathematical concepts. Furthermore, ethical considerations related to the responsible use of this visual encoding will be addressed. The discussion encompasses the potential for bias when choosing colors, especially when presenting data to diverse audiences. Finally, the future direction of visual number representation, including the impact of technology and the integration of new display technologies, will be considered.